티스토리 뷰
https://www.acmicpc.net/problem/14500
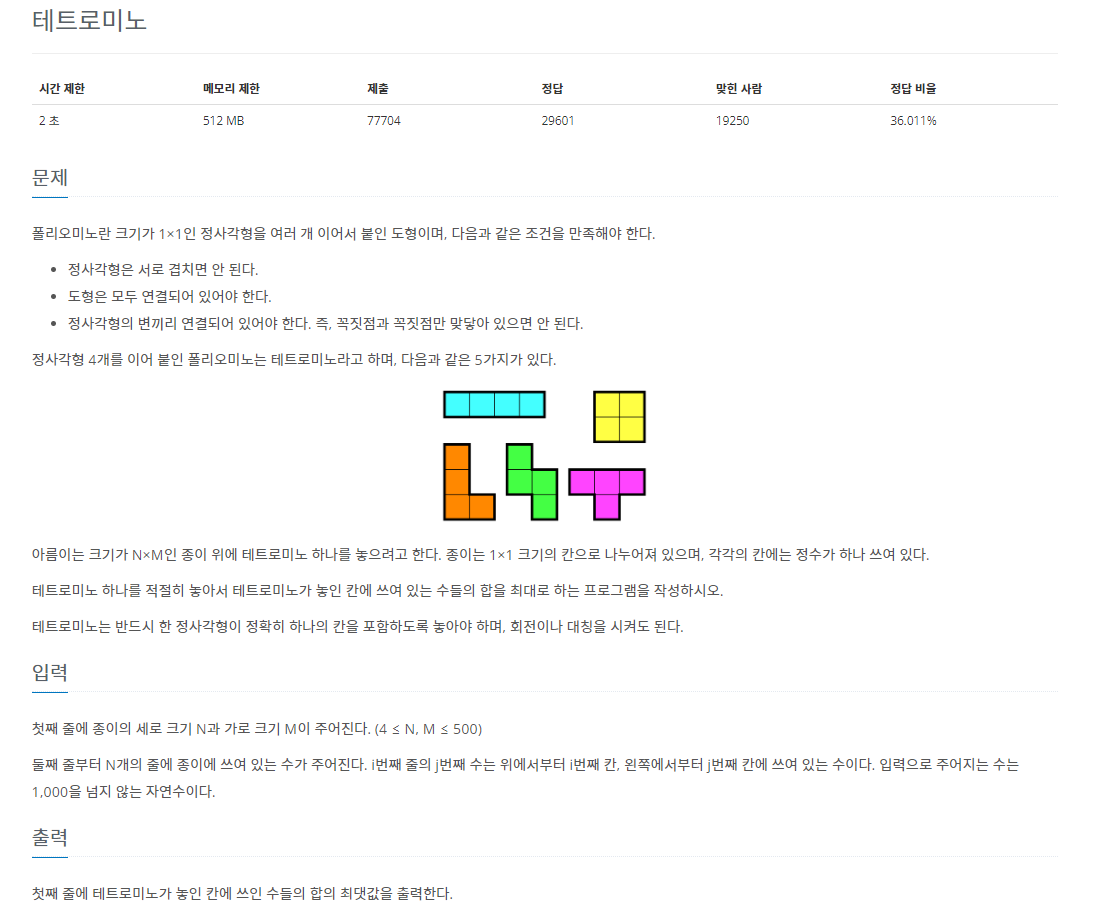
14500번: 테트로미노
폴리오미노란 크기가 1×1인 정사각형을 여러 개 이어서 붙인 도형이며, 다음과 같은 조건을 만족해야 한다. 정사각형은 서로 겹치면 안 된다. 도형은 모두 연결되어 있어야 한다. 정사각형의 변
www.acmicpc.net
문제 풀이
시간 복잡도를 계산하면 모든 점의 좌표에서 5가지 테트로미노의 회전과 대칭을 고려한 경우의 수를 모두 계산하므로 대략 n*m*5(5가지 테트로미노)*10(회전과 대칭을 고려했을 때 가능한 경우가 대략 10개 정도라고 가정)*4(4개의 정사각형) 정도가 된다. 즉 상한을 구하면 500 * 500 * 5 * 10 * 4 = 50,000,000으로 모든 경우를 2초안에 여유롭게 계산이 가능하다.
따라서 브루트포스로 풀 수 있음을 확인하고 풀이를 시작하였다.
1. 각 좌표에서 가능한 모든 테트로미노 경우의 수를 확인하여 최대값 갱신
이게 끝이다.
코드
#include <bits/stdc++.h>
using namespace std;
int board[501][501];
int n, m;
int ans;
vector<vector<vector<int>>> dx = {
{{0, 1, 2, 3},
{0, 0, 0, 0}},
{{0, 0, 1, 1}},
{{0, 0, 0, 1},
{0, 0, 1, 2},
{0, 0, 0, -1},
{0, 1, 2, 2},
{0, 1, 1, 1},
{0, 1, 2, 2},
{0, 0, 1, 2},
{0, 0, 0, 1}
},
{{0, 0, 1, 1},
{0, 0, -1, -1},
{0, 0, -1, 1},
{0, 1, 1, 2}},
{{0, 1, 1, 2},
{0, 0, -1, 1},
{0, 0, 0, 1},
{0, 0, 0, -1}
}};
vector<vector<vector<int>>> dy = {
{{0, 0, 0, 0},
{0, 1, 2, 3}},
{{0, 1, 0, 1}},
{{0, 1, 2, 2},
{0, 1, 0, 0},
{0, 1, 2, 2},
{0, 0, 0, 1},
{0, 0, 1, 2},
{0, 0, 0, -1},
{0, 1, 1, 1},
{0, 1, 2, 0}
},
{{0, 1, 1, 2},
{0, 1, 1, 2},
{0, 1, 1, 0},
{0, 0, 1, 1}},
{{0, 0, 1, 0},
{0, 1, 1, 1},
{0, 1, 2, 1},
{0, 1, 2, 1}
}
};
void check(int y, int x) { // (x, y)에서 가능한 5가지 테트리미노를 모두 확인한다.
for(int i=0; i<5; i++) {
for(int j=0; j < dx[i].size(); j++) {
int tmp = 0;
for(int k=0; k<dx[i][j].size(); k++) {
int nx = x + dx[i][j][k];
int ny = y + dy[i][j][k];
if(ny >= n || nx >= m || ny < 0 || nx < 0) {
tmp = 0;
break;
}
tmp += board[ny][nx];
}
ans = max(ans, tmp);
}
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> m;
for(int i=0; i<n; i++)
for(int j=0; j<m; j++)
cin >> board[i][j];
for(int i=0; i<n; i++) {
for(int j=0; j<m; j++) {
check(i, j);
}
}
cout << ans << '\n';
}하지만 위의 코드는 dy, dx를 틀리지 않게 잘 작성해야한다. 따라서 시간이 매우 오래걸렸다.
다른 풀이로는 DFS를 이용하여 4칸을 탐색하면 된다. 왜냐하면 한 좌표에서 4칸을 탐색하는 것과 한 좌표에서 테트로미노를 회전, 대칭시키는 것은 동치이기 때문이다. 즉, 4칸을 탐색하는 것을 테트로미노로 채울 수 있다.
여기서 ㅜ모양은 DFS로 탐색이 불가능하기 때문에 따로 처리를 해주었다.
구현한 코드는 다음과 같다.
#include <bits/stdc++.h>
using namespace std;
int board[501][501];
bool visited[501][501];
int n, m;
int ans;
int dx[] = {-1, 1, 0, 0};
int dy[] = {0, 0, -1, 1};
int tmp;
void dfs(int y, int x, int k) {
if(k == 3) {
ans = max(ans, tmp);
return;
}
for(int i=0; i<4; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
if(nx < 0 || ny < 0 || ny >= n || nx >= m || visited[ny][nx]) continue;
visited[ny][nx] = true;
tmp += board[ny][nx];
dfs(ny, nx, k+1);
tmp -= board[ny][nx]; // backtrack
visited[ny][nx] = false; // backtrack
}
// ㅜ, ㅗ, ㅏ, ㅓ가 보드판을 벗어나지 않는 범위에서 계산
if(y < n-1 && x < m-2) { // ㅜ
ans = max(ans, board[y][x] + board[y][x+1] + board[y][x+2] + board[y+1][x+1]);
}
if(y < n-1 && x > 0 && x < m-1) { // ㅗ
ans = max(ans, board[y][x] + board[y+1][x] + board[y+1][x-1] + board[y+1][x+1]);
}
if(y < n-2 && x < m-1) { // ㅏ
ans = max(ans, board[y][x] + board[y+1][x] + board[y+2][x] + board[y+1][x+1]);
}
if(y < n-2 && x > 0) { // ㅓ
ans = max(ans, board[y][x] + board[y+1][x] + board[y+1][x-1] + board[y+2][x]);
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> m;
for(int i=0; i<n; i++)
for(int j=0; j<m; j++)
cin >> board[i][j];
for(int i=0; i<n; i++) {
for(int j=0; j<m; j++) {
visited[i][j] = true;
tmp += board[i][j];
dfs(i, j, 0);
tmp -= board[i][j]; // backtrack
visited[i][j] = false; // backtrack
}
}
cout << ans;
}'알고리즘 > 브루트포스' 카테고리의 다른 글
| C++ 1248 Guess (0) | 2023.07.31 |
|---|---|
| C++ 14501 퇴사 (0) | 2023.07.29 |
| C++ 10972 다음 순열 (0) | 2023.07.29 |
| C++ 1748 수 이어 쓰기 1 (0) | 2023.07.27 |
| C++ 백준 1107 리모컨 (0) | 2023.07.23 |
